Emmanuel Klinger

Expectation Maximization in Python - Unsupervised Learning

My last post last post was about the theory of the expectation maximization algorithm. Here I provide a short and pythonic implementation for the case of a Gaussian mixture model. The first class I define is a class which represents a Gaussian component.

class Gauss:
    def __init__(self, mu, cov, pi):
        self.mu = mu
        self.cov = cov
        self.pi = pi
        self.r = None

    def __repr__(self):
        return "Gauss({}, {}, {})".format(self.mu, self.cov, self.pi)

    def p(self, x):
        return st.multivariate_normal.pdf(x, mean=self.mu, cov=self.cov)

    def expectation(self, X):
        self.r = self.pi * self.p(X)

    def maximization(self, X):
        self.maximize_pi()
        self.maximize_mu(X)
        self.maximize_sigma(X)

    def maximize_mu(self, X):
        self.mu = X.T @ self.r / self.r.sum()

    def maximize_sigma(self, X):
        x_minus_mu_weighted = (X - self.mu) * self.r[sp.newaxis].T
        self.cov = x_minus_mu_weighted.T @ x_minus_mu_weighted / self.r.sum()

    def maximize_pi(self):
        self.pi = self.r.mean()

Next, we need a class which represents the mixture. This class implements Python's list interface. And has a fit method which calls the expectation and maximization steps.

import scipy as sp
import scipy.stats as st

class Mixture:
    def __init__(self, components):
        self.components = list(components)

    def __repr__(self):
        return "{}({})".format(self.__class__.__name__, self.components)

    def __len__(self):
        return len(self.components)

    def __getitem__(self, item):
        return self.components[item]

    def expectation(self, X):
        for component in self:
            component.expectation(X)
        self._normalize_components()

    def _normalize_components(self):
        r_sum = sum(component.r for component in self)
        for component in self:
            component.r /= r_sum

    def maximization(self, X):
        for k, component in enumerate(self):
            component.maximization(X)

    def fit(self, X, n_steps=100):
        for _ in range(n_steps):
            self.expectation(X)
            self.maximization(X)

To check if and how it works I generate a data set with scikit-learn's make_blobs. I create a mixture consisting of three components and fit it to the data.

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

n_classes = 3
X, y = make_blobs(n_samples=100, centers=n_classes)

mixture = Mixture(Gauss(sp.randn(2) * 4, sp.eye(2), 1 / n_classes) for _ in range(n_classes))
mixture.fit(X)

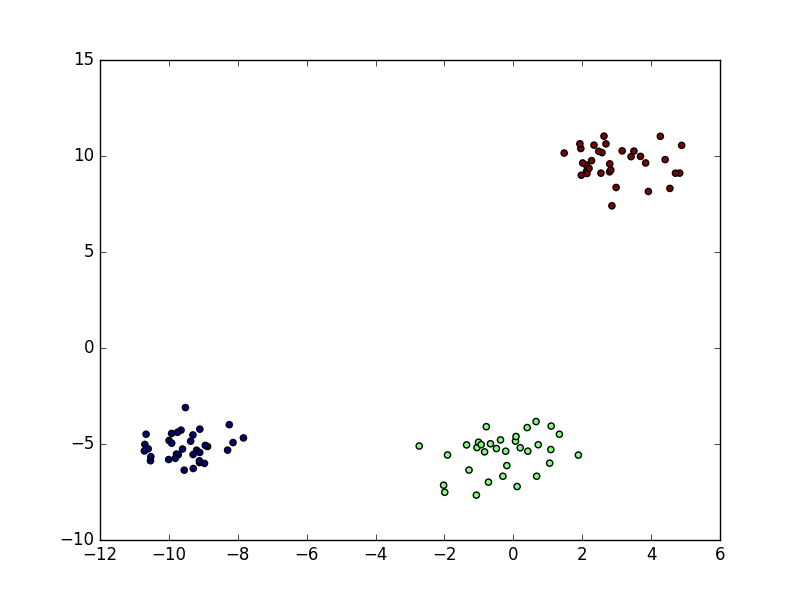
The original data consists of three clusters

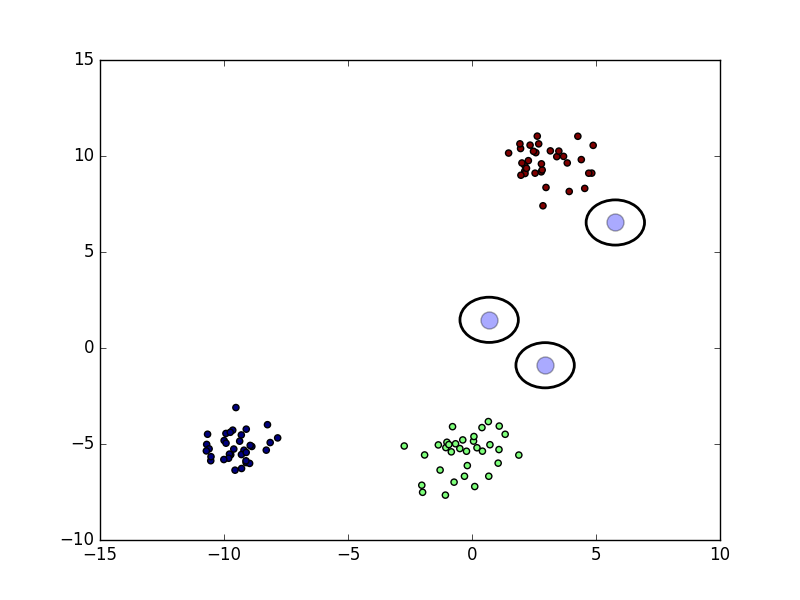
The Gaussians are initialized randomly. At the start of the algorithm they are really off

After 100 expectation-maximization steps they are fitted well to the data.

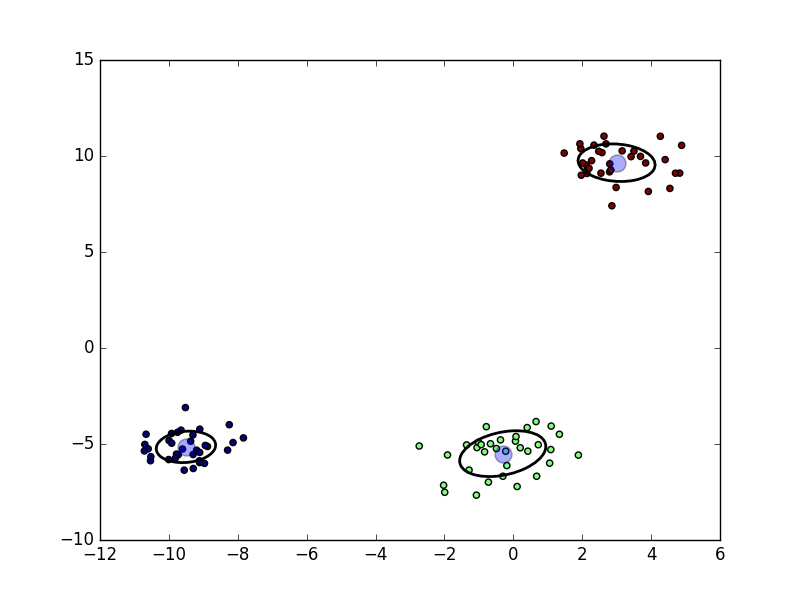
Here, the expectation-maximization algorithm was used for unsupervised probabilistic clustering.